The PID Controller

and its Software Implementation
a gentle introduction
ELE2024, Lecturer: P. Sopasakis
What is control?
a few examples...

Taking a Shower

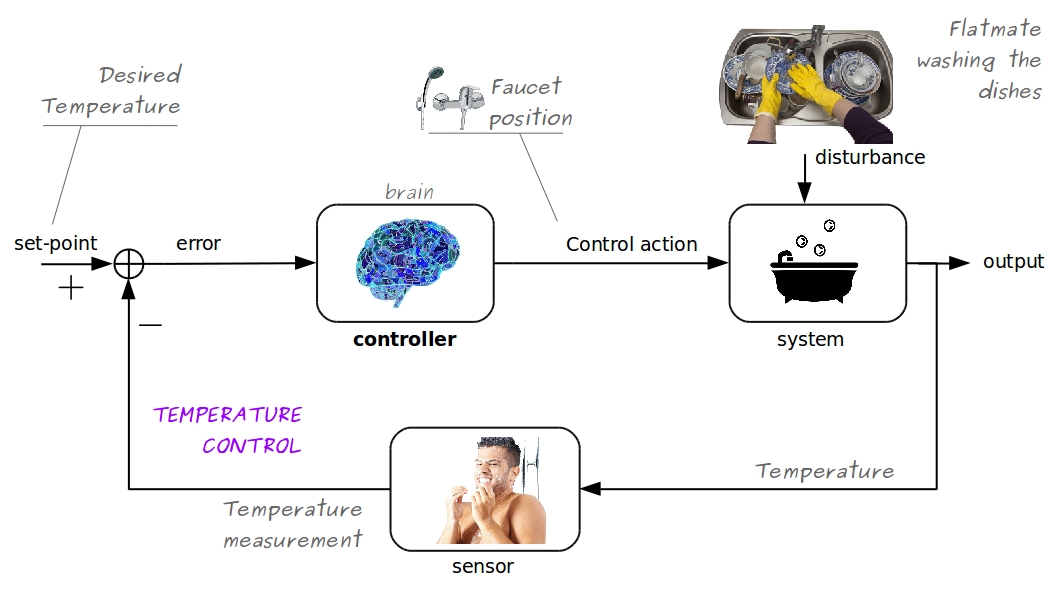
Define (error) = (set point) - (measurement), that is
$$e(t) = y^{\mathrm{sp}}(t) - y(t)$$
If $e(t){}={}0$ (perfect!) $\Rightarrow$ enjoy!
If $e(t){}>{}0$ (too cold!) $\Rightarrow$ warm up
If $e(t) {}<{} 0$ (too hot!) $\Rightarrow$ cool down

Speed Control

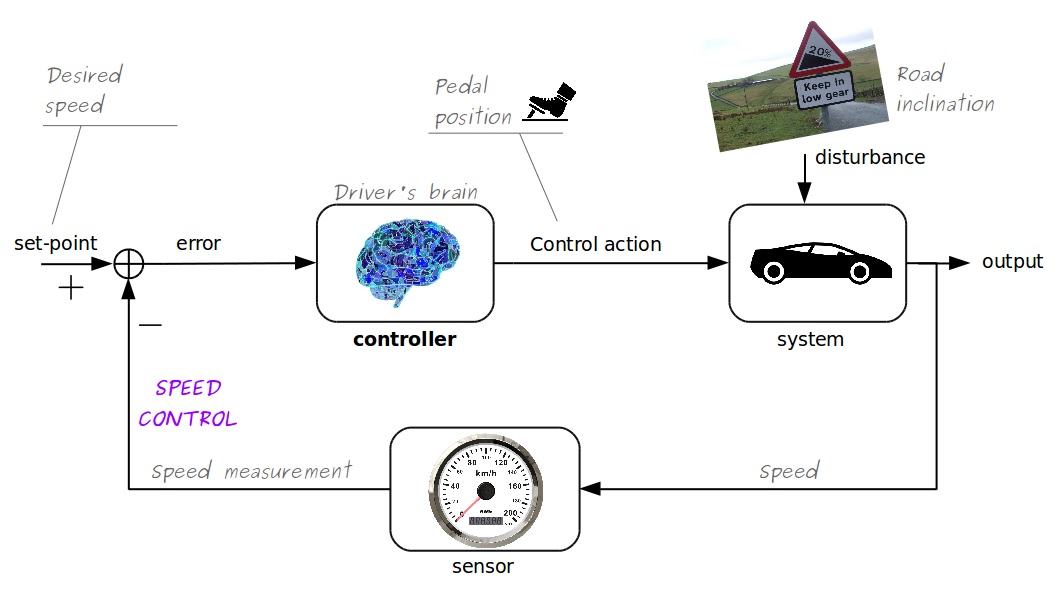
Define (error) = (set point) - (measurement), that is
$$e(t) = y^{\mathrm{sp}}(t) - y(t)$$
If $e(t){}={}0$ (perfect!) $\Rightarrow$ keep going!
If $e(t){}>{}0$ (too slow!) $\Rightarrow$ speed up
If $e(t) {}<{} 0$ (too fast!) $\Rightarrow$ slow down

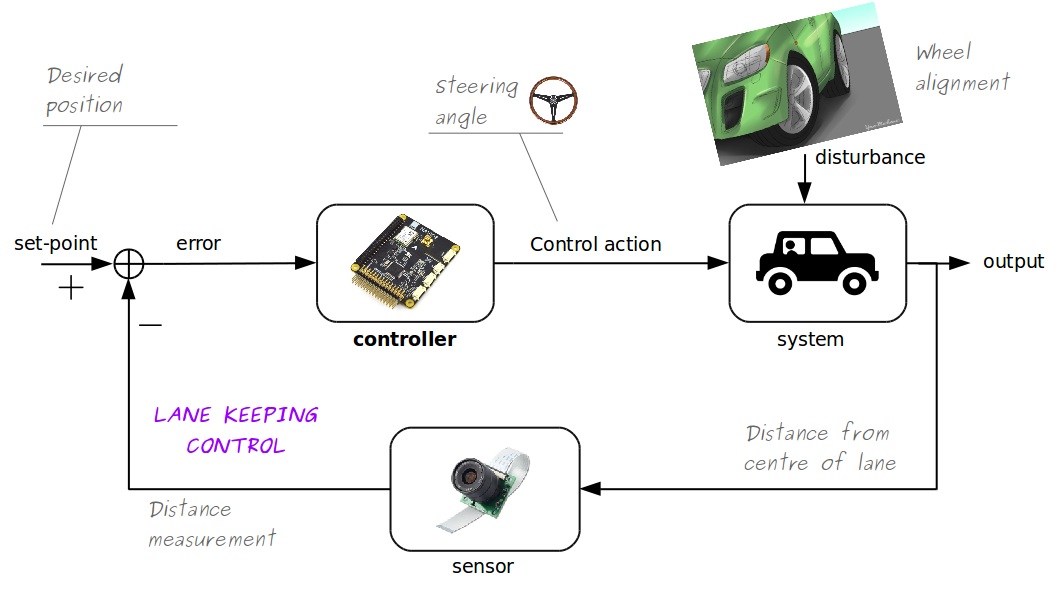
Lane Keeping

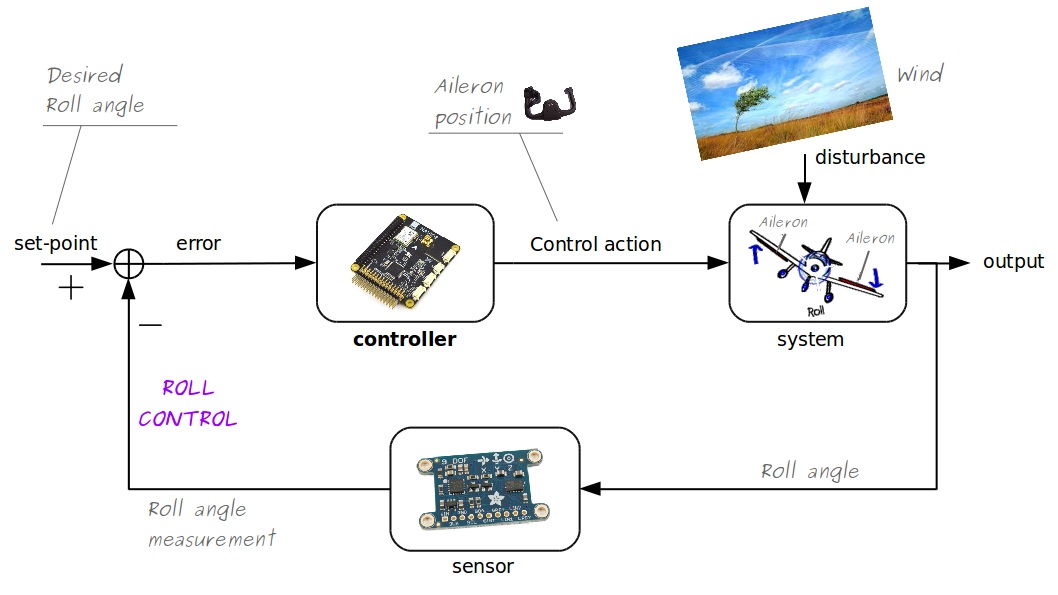
Aircraft Roll Control

Room temperature control

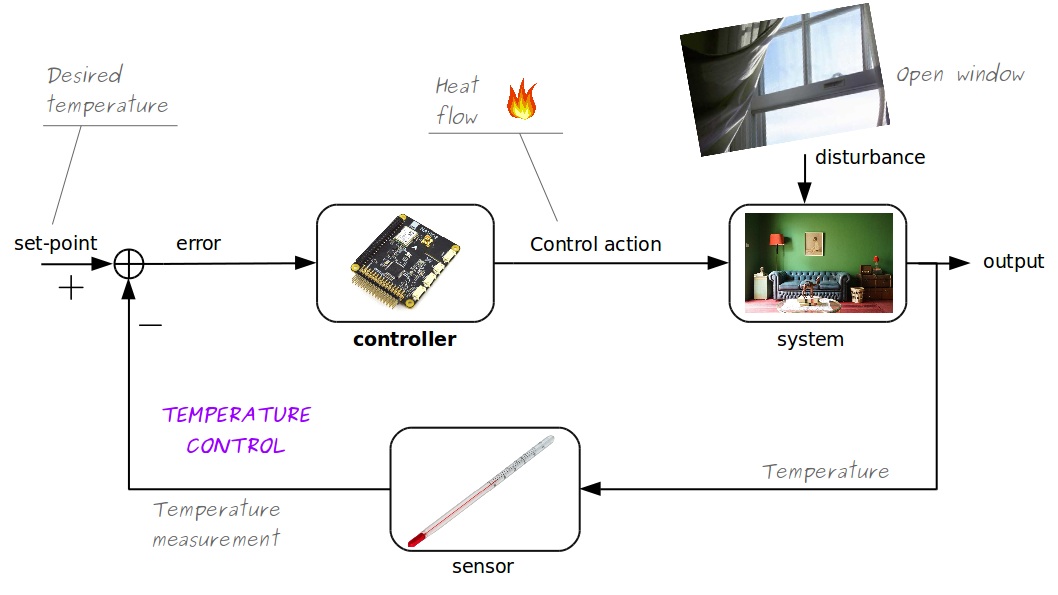
Lane Keeping Feedback Loop

  • System: car
  • Controlled variable (output): distance from centre of lane, $y(t)$
  • Sensor: camera
  • Set point: center of lane, $y^{\mathrm{sp}} = 0$
  • Error: $e(t) = -y(t)$
  • Control action: steering angle, $u(t)$
  • Disturbance: alignment of wheels
Lane Keeping Control
Autonomous Driving Technologies
  • Control theory
  • Image/video/signal processing
  • Machine learning
  • Optimisation
  • Computer science
  • Sensors
Autonomous Driving
Pros and Cons?

Challenges

  • Safety:
    • driving will be safer (hopefully)
    • robots don't drink/get tired/get distracted
  • Accountability and moral questions:
    • whose fault is it when autonomous cars crash?
    • insurance
  • Socioeconomic:
    • towards liberation from labour?
    • loss or creation of jobs?
  • Regulation:
    • is there need for traffic lights?
  • Accessibility:
    • accessible to disabled and elderly people
  • Reduced traffic, higher speeds
  • Environmental:
    • lower energy consumption
  • Security and Privacy:
    • continuous surveillance?
    • protection of personal data?
    • hacking
    • software reliability
The P-Controller
Proportional Controller
Steering is proportional to error
$$u(t) = K_p \cdot e(t)$$
Too slow! Let's increase $K_p$.
Too oscillatory!
What if we increase $K_p$ even more?
Increase $K_p$ for a faster response, which may lead to oscillations
The PD-Controller
Proportional-Derivative Controller
The control action is
$u(t)$ ${}={}$ $K_p e(t)$ ${}+{}$ $K_d \dot{e}(t)$
That's better!
Let's increase $K_d$ even more...
This is less oscillatory
Let's eliminate the oscillations!
By increasing $K_d$ we have eliminated the oscillations!
Increase $K_d$ to suppress the oscillations
Increase $K_p$ for a faster response, which may lead to oscillations
The PID-Controller
Proportional-Integral-Derivative Controller
Warning!
All models are wrong*
* George Box, 1976
Offset = $ \lim_{t\to\infty} e(t)$
We must eliminate the offset!
Define $I(t) = \int_0^t e(\tau)\mathrm{d}\tau$
The integral diverges
because $e(t)$ fails to converge to zero...
Let's plug the integral into the controller...
$u(t)$ ${}={}$ $K_p e(t)$ ${}+{}$ $K_d \dot{e}(t)$ ${}+{}$ $K_i I(t)$
No Offset!
Software Implementation of PID

Digital Control Systems

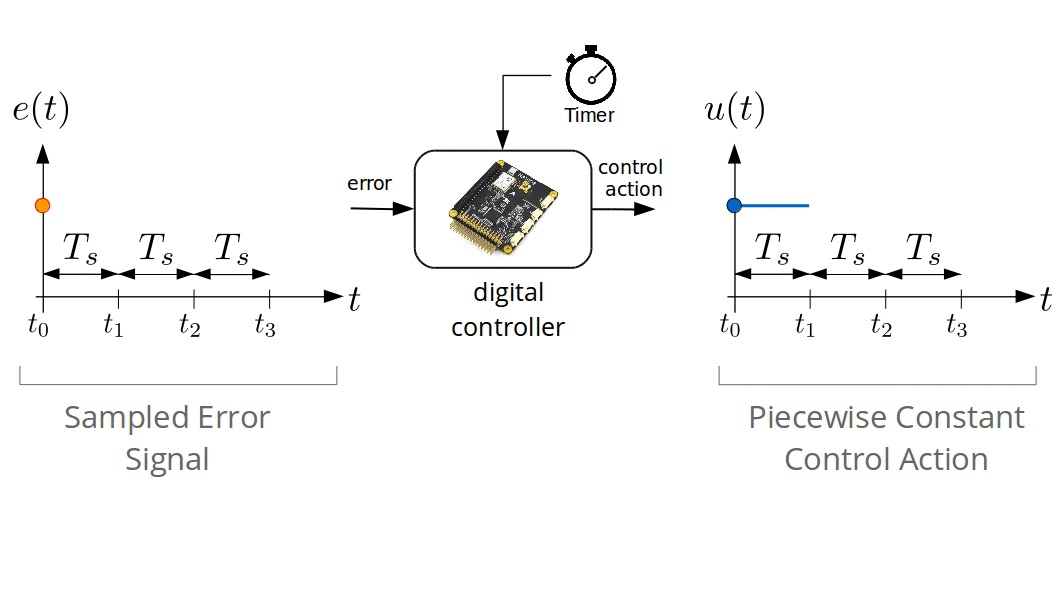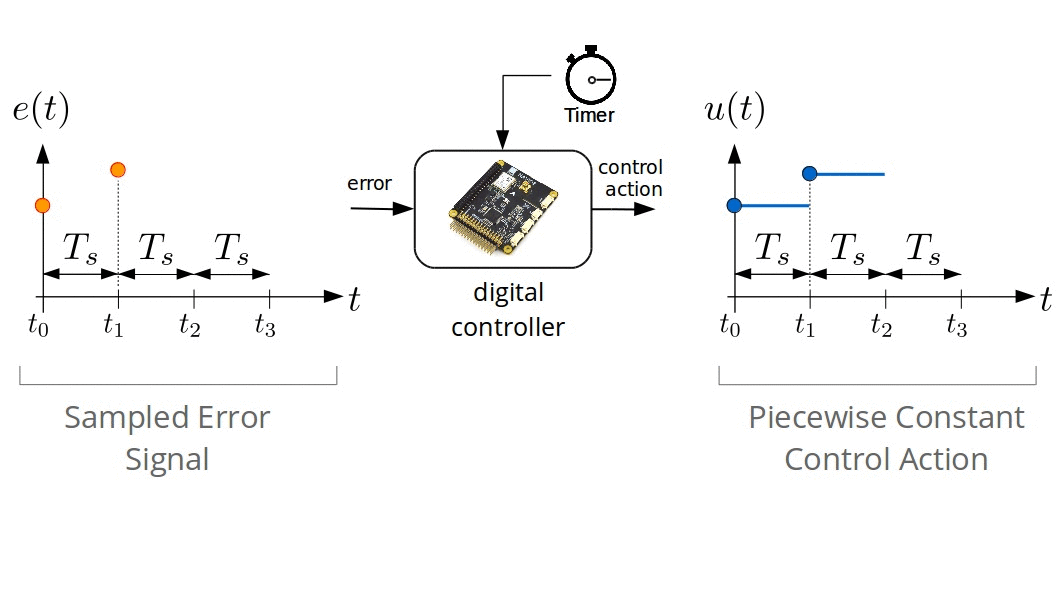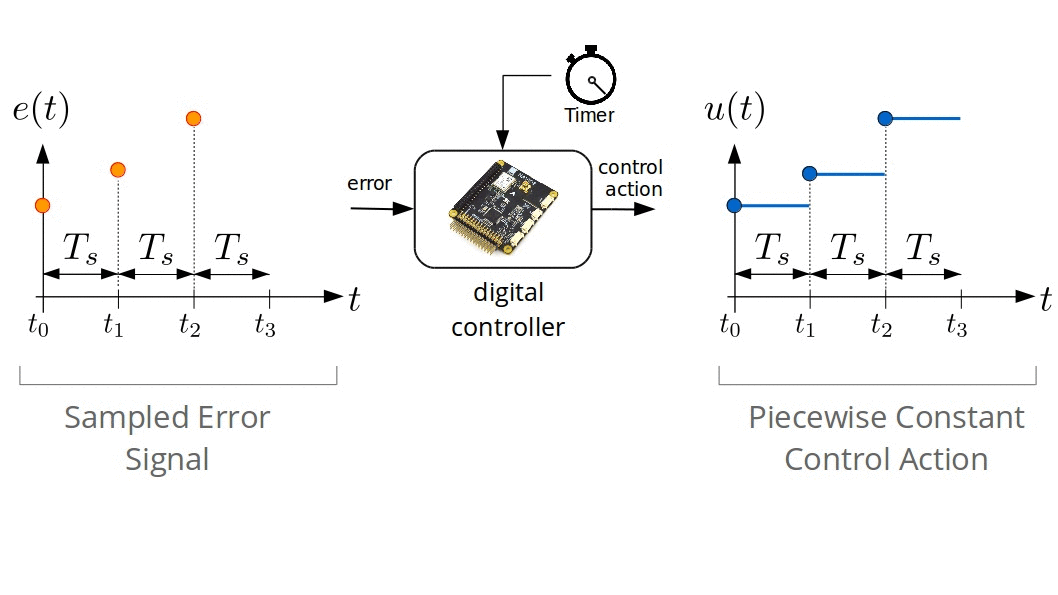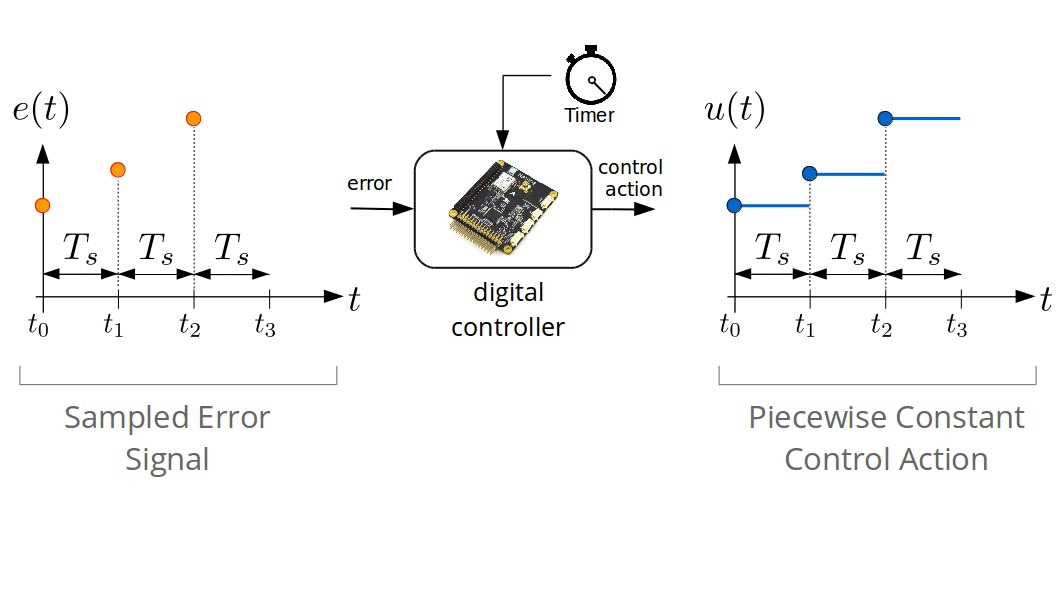
Digital Control Systems

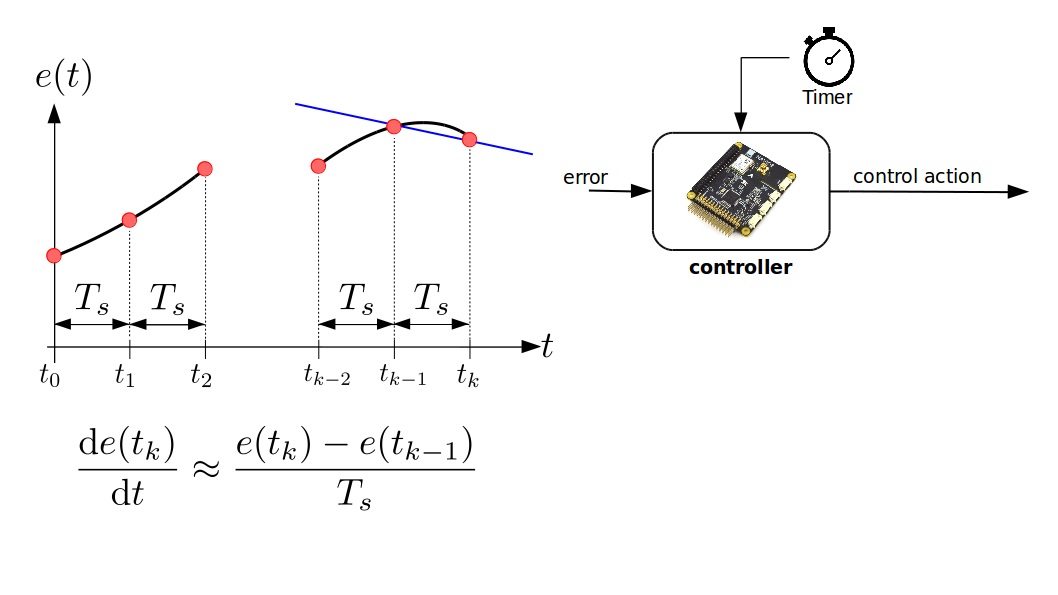
Digital Approximation of $\dot{e}(t)$

Digital Approximation of $I(t)$

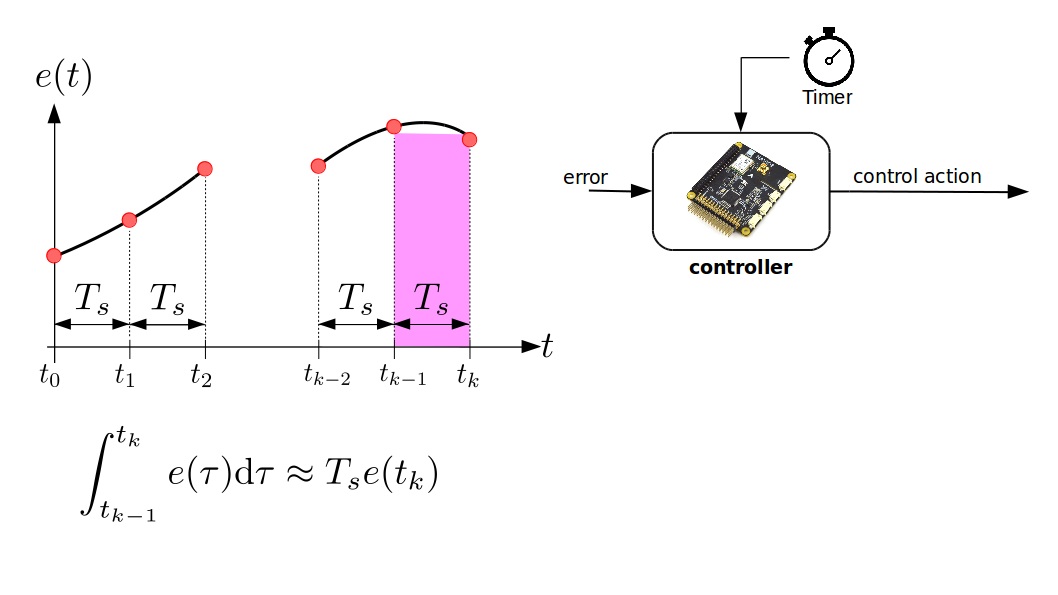
Trapezoidal rule

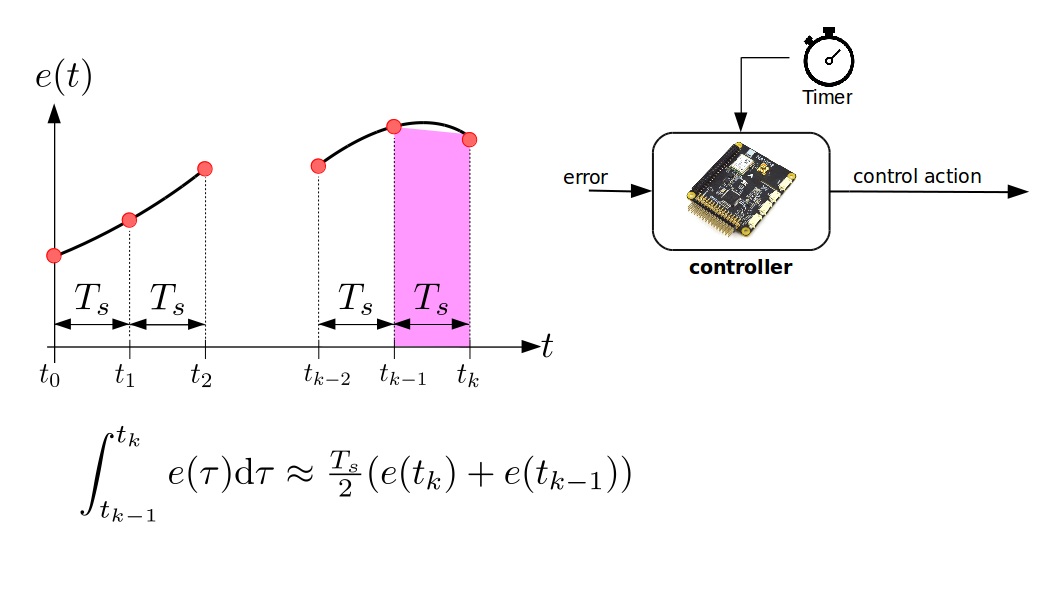
Digital Approximation of $I(t)$

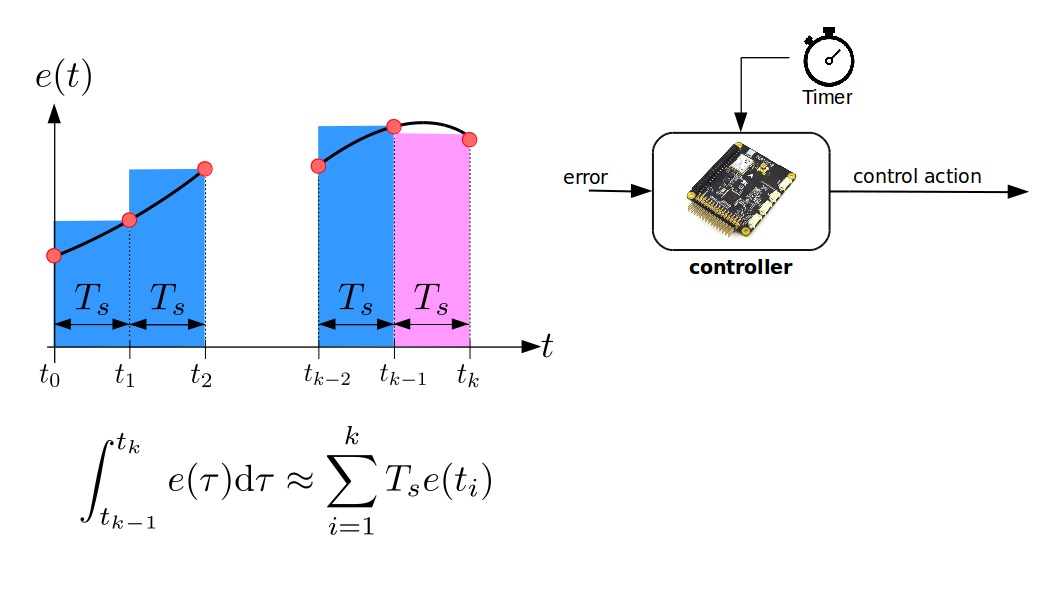
Discrete-time PID

Discrete-time PID controller
$\begin{align}u(t_k) ={}& \underbrace{K_p e(t_k)}_{\text{Prop.}} + \underbrace{K_d \frac{e(t_k) - e(t_{k-1})}{T_s}}_{\text{Deriv. Approx.}} + \underbrace{ K_i \sum_{i=1}^{k} T_s e(t_i) }_{\text{Integral Approx.}} \end{align}$

Discrete-time PID

Discrete-time PID controller
$\begin{align}u(t_k) ={}& K_p e(t_k) + K_d \frac{e(t_k) - e(t_{k-1})}{T_s} + K_i \sum_{i=1}^{k} T_s e(t_i)\\ ={}& K_p e(t_k) + {\color{blue}{K_{d, d}}} (e(t_k) - e(t_{k-1})) + {\color{red}{K_{i, d}}} \sum_{i=1}^{k}e(t_i) \end{align}$
where $K_{d, d} = \frac{K_d}{T_s}$ and $K_{i, d} = K_i T_s$.

PID implementation


            /* PID implementation (pseudocode) */          
            previous_error = 0.0, sum_error = 0.0;
  
            /* Initialise variables */                    
            previous_error = setpoint - measured_value;
            
            /* Call the following function at every sampling time */
            function compute_control_action(measured_value, setpoint) {
              ctrl_error = setpoint - measured_value;
              delta_error = ctrl_error - previous_error;
              control = P_GAIN_DISCRETE * ctrl_error 
                      + I_GAIN_DISCRETE * sum_error 
                      + D_GAIN_DISCRETE * delta_error;
              sum_error += ctrl_error;
              previous_error = ctrl_error;
              return control;
            }

Let's recap
Control loop - new terms:
  • system
  • controlled variable
  • sensor
  • measurement
  • set-point
  • error, $e(t) = y^{\mathrm{sp}}(t) - y(t)$
  • control action
  • controller
  • disturbance
PID controller:
  • P: proportional control action
  • D: suppresses oscillations
  • I: eliminates offset
Digital PID controller:
  • D: successive differences
  • I: sum of errors
Today's Lab
PID controller design for lane keeping

Objective

We will design and test a discrete-time PID controller in Python.

Python Programming
Why Python?
  • free
  • open source
  • easy
  • strong community
  • highly sought skill

Python in Engineering

  • Controller design
  • Simlations of dynamical systems
  • Optimisation
  • Image/video/signal processing
  • Machine learning
  • Parallel computing

Grading Criteria

  • Technical correctness (45%)
  • Discussion of the results (15%)
  • Quality of presentation (25%) Quality of presentation (25%): (i) clarity, (ii) graphics, (iii) typesetting
  • Quality of code (15%): (i) correctness, (ii) style, (iii) docs/comments
  • Bonus marks (+10%)
Deadline: Ten (calendar) days from now.
For best results: use the Overleaf template provided

Let's get started!

  • Start PyCharm
  • Create a new project (Python3.6 with virtualenv)
  • Go to File > Settings > Python Interpreter > Add:
    • numpy, v1.19
    • scipy, v1.5.0
    • matplotlib, v3.2.2