Opengen basics

We present opengen: a Python interface to Optimization Engine (OpEn), which facilitates the process of code generation of high-performance parametric optimizers.

OpEn functionality; high level diagram

About

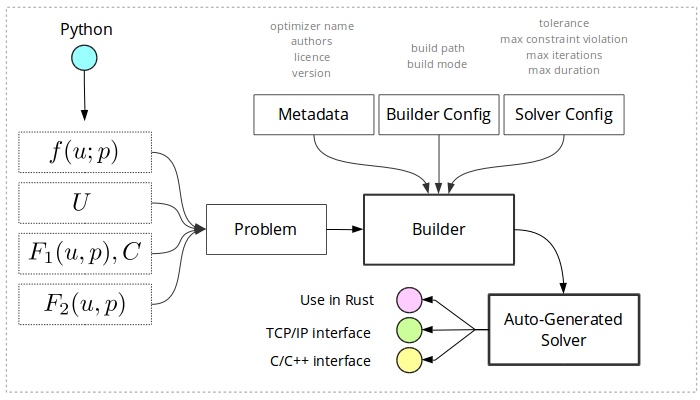
Opegen is a Python package that facilitates the design of parametric optimizers and generates Rust code using Optimization Engine. The user designs the parametric optimization problem entirely in Python. The auto-generated code is then compiled in Rust can be used in any of the following ways:

Directly in Rust (you can include it in you Rust project as a dependency)
Over a TCP socket based on JSON (which can be accessed easily from any programming language)
In Python (using the TCP/IP interface in the background)
In Python by accessing the Rust-based auto-generated optimizer directly
In C or C++ using auto-generated C/C++ bindings (header files and static or shared libraries)
In ROS using auto-generated ROS packages

Opengen code generation

Getting started

Problem specification

Here we will demonstrate how to use opengen to generate a parametric optimizer

\[\begin{split}\operatorname*{Minimize}_{u {}\in{} \mathbb{R}^{n_u}}&\ \ f(u, p)\\ \mathrm{subject\ to} &\ \ u \in U\end{split}\]

The first step is to import opengen and casadi in your Python code:

import casadi.casadi as cs
import opengen as og

Next, we define the cost function. Suppose that we want to minimize the Rosenbrock function defined as

\[f(u) = \sum_{i=1}^{n_u - 1} b (u_{i+1} - u_{i}^2)^2 + (a-u_i)^2\]

where $u=(u_1,\ldots, u_{n_u})$ is the decision variable and $p=(a, b)$ is a parameter vector.

Consider the case with $n_u=5$. The cost function is defined using CasADi SX symbols as follows:

u = cs.SX.sym("u", 5)                 # decision variable (nu = 5)
p = cs.SX.sym("p", 2)                 # parameter (np = 2)
phi = og.functions.rosenbrock(u, p)   # cost function

Constraints

Next, we need to define the constraints. OpEn supports the following types of constraints:

Constraint	Explanation
`AffineSpace`	An affine space is a set of the form $\{x\in\mathbb{R}^n {}:{} Ax = b\}$ for a matrix $A\in \mathbb{R}^p$ and vector $b$. Docs: (Rust, Python)
`Ball2`	Euclidean ball: `Ball2(None, r)` creates a Euclidean ball of radius `r` centered at the origin, and `Ball2(xc, r)` is a ball centered at point `xc` (list/np.array) Docs: (Rust, Python)
`BallInf`	Ball of infinity norm:`BallInf(None, r)` creates an infinity-norm ball of radius `r` centered at the origin, and `BallInf(xc, r)` is an infinity ball centered at point `xc` (list/np.array) Docs: (Rust, Python)
`Ball1`	L1 ball: `Ball(None, r)` creates an ell1-ball of radius `r` centered at the origin, and `BallInf(xc, r)` is an ell1-ball centered at point `xc` (list/np.array) Docs: (Rust, Python)
`Sphere2`	Euclidean sphere: `Sphere2(None, r)` creates a Euclidean sphere of radius `r` centered at the origin, and `Sphere2(xc, r)` is a sphere centered at point `xc` (list/np.array) Docs: (Rust, Python)
`Simplex`	A simplex of size $\alpha$ is a set of the form $\Delta_\alpha = \{x \in \mathbb{R}^n {}:{} x_i \geq 0, \sum_i x_i = \alpha\}$. Create one with `Simplex(alpha)`. Projections are computed using Condat's fast projection method. Docs: (Rust, Python)
`Halfspace`	A halfspace is a set of the form $\{u \in \mathbb{R}^{n_u} {}:{} \langle c, u\rangle \leq b \}$, for a vector $c$ and a scalar $b$. The syntax is straightforward: `Halfspace(c, b)`. Docs: (Rust, Python)
`Hyperplane`	A hyperplane is a set given by $H=\{x \in \mathbb{R}^n {}:{} c^\intercal x =b \}$. Docs: Rust
`FiniteSet`	Finite set, $\{u^{(1)},\ldots,u^{(m)}\}$; the set of point is provided as a list of lists, for example, `FiniteSet([[1,2],[2,3],[4,5]])`. The commonly used set of binary numbers, $\{0, 1\}$, is created with `FiniteSet([[0], [1]])`. Docs: (Rust, Python)
`NoConstraints`	No constraints - the whole $\mathbb{R}^{n}$ Docs: (Rust, Python)
`Rectangle`	Rectangle, $$R = \{u \in \mathbb{R}^{n_u} {}:{} f_{\min} \leq u \leq f_{\max}\},$$ for example, `Rectangle(fmin, fmax)` Docs: (Rust, Python)
`SecondOrderCone`	Second-order aka "ice cream" aka "Lorenz" cone. Docs: (Rust, Python)
`EpigraphSquaredNorm`	The epigraph of the squared Euclidean norm is a set of the form $X = \{(z, t) \in \mathbb{R}^{n+1}: \Vert z \Vert \leq t\}$. Docs: (Rust, Python: to be implemented)
`CartesianProduct`	Cartesian product of any of the above. See more information below. Docs: (Rust, Python)
`Zero`	The set $\{0\}$. Docs: (Rust, Python)

Cartesian Product

A Cartesian product is a set $C = C_0 \times C_1 \times \ldots \times C_{s}$. In $\mathbb{R}^n$, a vector $x$ can be segmented as $$x=(x_{(0)}, x_{(1)}, \ldots, x_{(s)}),$$ into $s$ segments, $x_{(i)}\in\mathbb{R}^{m_i}$. The constraint $x \in C$ means $$x_{(i)} \in C_i,$$ for all $i=0,\ldots, s$. For example, consider the vector $x = ({\color{blue}{x_0}}, {\color{blue}{x_1}}, {\color{red}{x_2}}, {\color{red}{x_3}}, {\color{red}{x_4}})$; define the segments $$x_{(0)} = ({\color{blue}{x_0}}, {\color{blue}{x_1}}),\ x_{(1)} = ({\color{red}{x_2}}, {\color{red}{x_3}}, {\color{red}{x_4}})$$ These can be identified by the indices 1 and 4 (last indices of segments).

Let us give an example: we will define the Cartesian product of a ball with a rectangle. Suppose that $U$ is a Euclidean ball with radius $r=1.5$ centered at the origin,

$$B^r_{\scriptsize \Vert{}\cdot{}\Vert_2}= \{u \in \mathbb{R}^2 {}:{} \Vert{}u\Vert {}\leq{} r \}.$$

This is,

ball = og.constraints.Ball2(None, 1.5)  # ball centered at origin

Consider now the following rectangle

rect = og.constraints.Rectangle(xmin=[-1,-2,-3], xmax=[0, 10, -1])

We can now construct the Cartesian product of these constraints. As discussed in the above table, it is

# Segments: [0, 1], [2, 3, 4]
segment_ids = [1, 4]
bounds = og.constraints.CartesianProduct(segment_ids, [ball, rect])

Problem Formulation

We may now define the optimization problem as follows:

problem = og.builder.Problem(u, p, phi)  \
        .with_constraints(bounds)

Opegen supports more general constraints of the form $F_2(u, p) = 0$ and $F_2(u, p) \leq 0$ (see next section).

Code generation

In order to generate a parametric optimizer in Rust for the above problem we need to specify the following information which, albeit optional, will need to be configured and customized in most cases

Metadata: general metadata about the auto-generated solver; The most important piece of information here is the optimizer_name. The optimizer will be stored in a folder with the same name
Build configuration: build options such as the path where the generated optimizer should be stored and the build mode (debug or release)
Solver configuration: solver-specific parameters such as the tolerance, L-BFGS memory length and more

Here is an example of metadata:

meta = og.config.OptimizerMeta()                \
    .with_version("0.0.0")                      \
    .with_authors(["P. Sopasakis", "E. Fresk"]) \
    .with_licence("CC4.0-By")                   \
    .with_optimizer_name("the_optimizer")

Info: Note that with_authors takes a list of strings. The licence is either the name of a licence or a URL. The optimizer name is the name of the auto-generated crate and the name of the folder in which all generated files will be stored.

Next, let us create a basic build configuration:

build_config = og.config.BuildConfiguration()  \
    .with_build_directory("python_build")      \
    .with_build_mode("debug")                  \
    .with_tcp_interface_config()

Method .with_tcp_interface_config() will activate the generation of a TCP/IP interface with which we will be able to call the solver from Python and other languages. You do not need to activate it if you plan to use the optimizer on an embedded device.

Info: You may configure the TCP parameters of the server by providing to .with_tcp_interface_config() a TcpServerConfiguration object. By default, the server will bind on 127.0.0.1 and will listen for requests at port 8333. See the advanced options for details.

This will instruct opegen to store the generated optimizer in python_build/the_optimizer. The build mode can be either debug (fast compilation, suboptimal performance) or release (slow compilation, best performance).

There are some additional parameters one might be interested in such as with_rebuild(True|False) (whether to re-build the optimizer from scratch - equivalent of clean+build).

Lastly, one needs to specify certain solver parameters; an example is given below:

solver_config = og.config.SolverConfiguration()   \
            .with_lbfgs_memory(15)                \
            .with_tolerance(1e-5)                 \
            .with_max_inner_iterations(155)

Method .with_max_inner_iterations is used to specify the maximum number of iterations. We refer to it as "inner" iterations to distinguish from "outer" iterations in the penalty method (see below).

We are now ready to call the code generator providing the above information:

builder = og.builder.OpEnOptimizerBuilder(problem,
                                          metadata=meta,
                                          build_configuration=build_config,
                                          solver_configuration=solver_config)
builder.build()

General constraints

OpEn can handle constraints of the general form

\[F_1(u, p) \in C,\tag{aLC}\]

where $F_1:\mathbb{R}^{n_u}\times \mathbb{R}^{n_p} \to\mathbb{R}^{n_1}$ is a smooth mapping and $C$ is a closed convex set. These constraints are handled with the augmented Lagrangian method and are tagged aLC.

OpEn can also handle constraints of the following form

\[F_2(u, p) = 0,\tag{PC}\]

where $F_2:\mathbb{R}^{n_u}\times\mathbb{R}^{n_p} \to\mathbb{R}^{n_2}$, using the penalty method. These constraints will be referred to as PC.

In most cases, the user can encode constraints in either the form of aLC or PC. However, the augmented Lagrangian method typically leads to better performance. The user can also use both types of constraints simultaneously.

Augmented Lagrangian Method

OpEn supports constraints of the aLC type. By choosing different sets $C$, the user can model a very wide range of constraints. For example,

Equality constraints, $F_1(u, p) = 0$ can be described by taking $C= \{0\}$, which corresponds to set Zero in Python
Element-wise constraints of the form $$ f_{\min} \leq F_1(u, p) \leq f_{\max}, $$ can be described by taking $C$ to be a Rectangle. Note that some elements of $f_{\min}$ and $f_{\max}$ can be set to $-\infty$ and $+\infty$ respectively
Norm constraints of the form $$\Vert F_1(u, p) \Vert \leq c$$ can be described by taking $C = B_{\Vert\cdot\Vert}^{c}$, where $\Vert{}\cdot{}\Vert$ can be either the Euclidean norm or the infinity norm (that is, Ball2 and BallInf)

As an example, consider the constraints

\[ \begin{split} 1.5u_1 {}={}& u_2 \\ \sin(u_3 + \pi/5) {}={}& 0.5 \end{split}\]

We select

\[ F_1(u, p) = \begin{bmatrix} 1.5u_1 - u_2 \\ \sin(u_3 + \pi/5) - 0.5 \end{bmatrix}\]

and

$$ C = \{0\}. $$

We may also to provide a compact set $Y \subseteq C^*$ (if we do not, this will be computed automatically); we select

$$Y = \{y \in \mathbb{R}^{n_1}{}:{} \Vert y \Vert_{\infty} \leq 10^{12}\}.$$

Now, the problem formulation becomes

f1 = cs.vertcat(1.5 * u[0] - u[1], cs.sin(u[2] + cs.pi/5) - 0.5)
set_c = og.constraints.Zero()
set_y = og.constraints.BallInf(None, 1e12)

and

problem = og.builder.Problem(u, p, phi)\
    .with_aug_lagrangian_constraints(f1, set_c, set_y)\  
    .with_constraints(bounds)

We can now generate a solver and solve the problem exactly as before. The solution is a pair $(u^\star, y^\star)$ given by

{
    "exit_status": "Converged",
    "num_outer_iterations": 9,
    "num_inner_iterations": 85,
    "last_problem_norm_fpr": 8.879341428457282e-06,
    "delta_y_norm_over_c": 7.147511762156759e-06,
    "f2_norm": 0.0,
    "solve_time_ms": 13.569209,
    "penalty": 78125.0,
    "solution": [
        0.018786377508686856,
        0.028186552233630396,
        -0.10471801035932687,
        0.02921323766336347,
        0.0007963509453450717
    ],
    "lagrange_multipliers": [
        0.7699528316368849,
        14.491152879893193
    ]
}

Penalty Method

Opengen can handle more general constraints of the form $F_2(u, p) = 0$ using the penalty method In particular, opengen can solve problems of the form

\[\begin{split} \operatorname*{Minimize}_{u {}\in{} \mathbb{R}^{n_u}}& \ f(u; p)\\ \mathrm{subject\ to}\, &u \in U, \\ &F_2(u, p) = 0,\end{split}\]

where $F_2:\mathbb{R}^{n_u}\times \mathbb{R}^{n_p} \to \mathbb{R}^{n_c}$.

This can be used to encode either equality or inequality constraints of the form $h(u, p) \leq 0$ using

\[F_2(u, p) = \max\{0, h(u, p)\}.\]

As an example, consider again the problem of minimizing the Rosenbrock function subject to the constraints

\[\begin{split} 1.5u_1 - u_2 {}={}& 0,\\ u_3 - u_4 + 0.1 {}\leq{}& 0. \end{split}\]

To that end, we define the constraints function

\[F_2(u, p) = \begin{bmatrix} 1.5u_1 - u_2 \\ \max\{0, u_3 - u_4 + 0.1\} \end{bmatrix}.\]

It is now very easy to include this in out problem formulation. We first need to define function $c$:

f2 = cs.vertcat(1.5 * u[0] - u[1],
                cs.fmax(0.0, u[2] - u[3] + 0.1))

and include it in the problem formulation:

problem = og.builder.Problem(u, p, phi)  \
    .with_penalty_constraints(f2)        \
    .with_constraints(bounds)

The rest of the code remains the same. The solution will now be

{
  "exit_status": "Converged",
  "num_outer_iterations": 6,
  "num_inner_iterations": 35,
  "last_problem_norm_fpr": 3.1976300788348913e-06,
  "max_constraint_violation": 7.659485695667156e-05,
  "solve_time_ms": 3.842833,
  "solution": [
    0.02196420476411661,
    0.032927537058737015,
    -0.031152544256866314,
    0.06877086088617702,
    0.004151858447457505 ]
}

Note here that the solver performed 6 outer penalty-type iterations and 35 inner iterations overall. The infinity norm of the constraint violations is approximately $7.66\cdot 10^{-5}$ (which is below the default tolerance of $10^{-4}$.) This means that the solution $u^\star$ satisfies

\[ \|c(u^\star, p)\|_{\infty}\leq 7.66\cdot 10^{-5}. \]

The user may change the maximum constraint violation using

solver_config.with_delta_tolerance(1e-6)

Calling the optimizer locally

Provided you have generated code using .with_tcp_interface_config(), you will be able to call it from Python.

All you need to do is create an instance of OptimizerTcpManager providing the path to your optimizer.

The typical steps involved in calling an optimizer over its TPC/IP interface are:

Start the server (starts in a separate thread and runs as a sub-process in the background)
Consume it
Stop it

The following code snippet should be self explanatory

mng = og.tcp.OptimizerTcpManager('python_build/the_optimizer')
mng.start()

pong = mng.ping()                 # check if the server is alive
print(pong)
response = mng.call([1.0, 50.0])  # call the solver over TCP


if response.is_ok():
    # Solver returned a solution
    solution_data = response.get()
    u_star = solution_data.solution
    exit_status = solution_data.exit_status
    solver_time = solution_data.solve_time_ms
else:
    # Invocation failed - an error report is returned
    solver_error = response.get()
    error_code = solver_error.code
    error_msg = solver_error.message


mng.kill()

The ping will return the dictionary {"Pong" : 1}. This is to check whether the server is alive.

As shown above, we then call the optimizer (over a TCP socket) and we provide the value of its parameter vector (here, [1.0, 50.0]). The solver returns a response object of type SolverResponse which is equipped with the following methods:

Method	Explanation
`is_ok()`	Whether the request was successful (`True`/`False`);
`get()`	Obtain a `SolverStatus` object if the request is successful (i.e., if `is_ok()` returns `True`) and an instance of `SolverError` otherwise

Note: Method is_ok returns True iff the server is successful in returning a solution - even if it has not converged (e.g., due to reaching the maximum number of iterations). The method returns False, only if the server is unable to compute any solution (e.g., if it gets into NaN).

If the TCP request is successful, method get() returns a SolverStatus, which is an object with the following properties:

Property	Explanation
`exit_status`	Exit status; can be (i) `Converged` or (ii) `NotConvergedIterations`, if the maximum number of iterations was reached, therefore, the algorithm did not converge up to the specified tolerances, or (iii) `NotConvergedOutOfTime`, if the solver did not have enough time to converge
`num_outer_iterations`	Number of outer iterations
`num_inner_iterations`	Total number of inner iterations (for all inner problems)
`last_problem_norm_fpr`	Norm of the fixed-point residual of the last inner problem; this is a measure of the solution quality of the inner problem
`f1_infeasibility`	Euclidean norm of $c^{-1}(y^+-y)$, which is equal to the distance between $F_1(u, p)$ and $C$ at the solution
`f2_norm`	Euclidean norm of $F_2(u, p)$ at the solution
`solve_time_ms`	Total execution time in milliseconds
`penalty`	Last value of the penalty parameter
`solution`	Solution
`cost`	Cost function at solution
`lagrange_multipliers`	Vector of Lagrange multipliers (if $n_1 > 0$) or an empty vector, otherwise

If, instead, the request is unsuccessful (e.g., if the wrong number of parameters is provided), a SolverError is returned by get(). This is an error report: an object with two properties: the error code and the error message.