Tandem tanks

Problem statement

Before we start

We will need to import the following libraries in Python:

import casadi.casadi as cs
import opengen as og
import matplotlib.pyplot as plt
import numpy as np

System dynamics

Consider the following system of tandem tanks

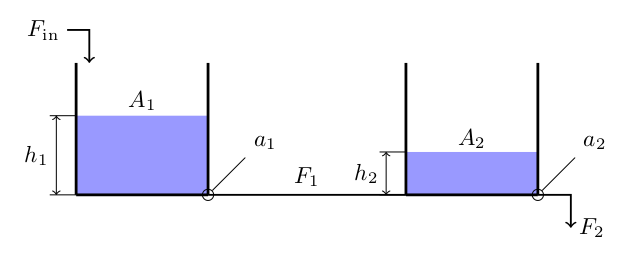
the tanks have cross-section areas $A_1$ and $A_2$, they store a liquid of density $\rho$ which can flow between the two tanks through a short pipe of cross-section area $a_1$. The liquid outflows from the second tank through an orifice of area $a_2$. The level of liquid in the two tanks, $h_1$ and $h_2$ is governed by the differential equations

\[ \begin{align} \dot{h}_1 {}={}& \tfrac{1}{\rho A_1} F_{\mathrm{in}} - \tfrac{a_1}{A_1}\sqrt{2g(h_1 - h_2)} \\ \dot{h}_2 {}={}& \tfrac{a_1}{A_1}\sqrt{2g(h_1 - h_2)} - a_2\sqrt{2gh_2} \end{align} \]

so long as $h_1 > h_2$.

This is a continuous-time dynamical system of the form

\[ \dot{x} = f(x, u), \]

where $x=(h_1, h_2)$ is the system state and $u=F_{\mathrm{in}}$ is the manipulated variable. The system parameters are

a1 = 10*1e-4
a2 = 10*1.5e-4
A1 = 2.5
A2 = 0.1
rho = 998
g = 9.8044
sampling_time = 15
nx = 2

and the continuous-time system dynamics is

def dynamics_ct(x, u):
    h1 = x[0]
    h2 = x[1]
    dx1 = u/(rho * A1) - (a1 / A1) * cs.sqrt(2 * g * (h1 - h2))
    dx2 = (a1 * cs.sqrt(2 * g * (h1 - h2)) - a2 * cs.sqrt(h2))/A2
    return [dx1, dx2]

We may discretize the system dynamics using, for example, the Euler discretization with sampling time $T_s$, that is, the discrete-time dynamics can be approximated by

\[ x_{t+1} = x_t + T_s f(x_t, u_t). \]

Let us write a little Python function for the discrete-time dynamics of the system

def dynamics_dt(x, u):
    dx = dynamics_ct(x, u)
    return [x[i] + sampling_time * dx[i] for i in range(nx)]

Nonlinear MPC problem

We shall construct a nonlinear MPC controller that drives the ball to the reference position $x_1^{\mathrm{ref}}=0$, i.e., at the reference state $x^{\mathrm{ref}}=(0,0,0,0)$ with input reference $u^{\mathrm{ref}}=0$.

To that end, let us define a state cost function $\ell(x, u)$ and a terminal cost function $\ell_N(x)$ as follows

\[ \begin{align} \ell(x, u) {}={}& \sum_{i=1}^{4}q_ix_i^2 + ru^2 \\ \ell_N(x) {}={}& \sum_{i=1}^{4}q_i^N x_i^2 \end{align} \]

In particular, let

q1 = 1
q2 = 1
qF = 0.5

qN1 = 50
qN2 = 50

def stage_cost(x, u):
    h1 = x[0]
    h2 = x[1]
    return q1 * (h1 - h1_ref)**2 + q2 * (h2 - h2_ref)**2 + qF * (u - F_ref)**2

def terminal_cost(x):
    h1 = x[0]
    h2 = x[1]
    return qN1 * (h1 - h1_ref)**2 + qN2 * (h2 - h2_ref)**2

The total cost function of the model predictive controller, along a prediction horizon $N$ will be

\[ V(x_0, u_0, \ldots, u_{N-1}) = \sum_{t=0}^{N-1}\ell(x_t, u_t) + \ell_N(x_N) \]

where $x_0$ is the given current state and $x_{t+1} = x_t + T_sf(x_t, u_t)$ as discussed above.

u_seq = cs.MX.sym("u", N)  # sequence of all u's
x0 = cs.MX.sym("x0", nx)   # initial state

x_t = x0
total_cost = 0
for t in range(0, N):
    total_cost += stage_cost(x_t, u_seq[t])  # update cost
    x_t = dynamics_dt(x_t, u_seq[t])         # update state

total_cost += terminal_cost(x_t)  # terminal cost

Lastly, we will impose the following input constraints

\[ 8 \leq u_t \leq 11 \]

for all $t=0,\ldots,N-1$. For that purpose, we shall define the following set

U = og.constraints.Rectangle([8]*N, [11]*N)

Code generation

We may now specify the problem and generate code

problem = og.builder.Problem(u_seq, x0, total_cost)  \
            .with_constraints(U)

build_config = og.config.BuildConfiguration()  \
    .with_build_directory("python_build")      \
    .with_tcp_interface_config()

meta = og.config.OptimizerMeta().with_optimizer_name("ball_and_plate")

solver_config = og.config.SolverConfiguration()\
    .with_tolerance(1e-6)\
    .with_initial_tolerance(1e-6)

builder = og.builder.OpEnOptimizerBuilder(problem, meta,
                                          build_config, solver_config)
builder.build()

This will generate a solver in Rust as well as a TCP server that will listen for requests at localhost:8333 (this can be configured).

Simulations

Closed-loop trajectories

We can now easily call the auto-generated solver through its TCP socket in a few lines of code:

# Create a TCP connection manager
mng = og.tcp.OptimizerTcpManager("python_build/ball_and_plate")

# Start the TCP server
mng.start()

# Run simulations
x_state_0 = [0.1, -0.05, 0, 0.0]
simulation_steps = 2000

state_sequence = x_state_0
input_sequence = []

x = x_state_0
initial_guess = None
for k in range(simulation_steps):
    solver_status = mng.call(x, initial_guess)
    us = solver_status['solution']
    u = us[0]
    initial_guess = us[1:] + [us[N-1]]
    x_next = dynamics_dt(x, u)
    state_sequence += x_next
    input_sequence += [u]
    x = x_next

# Thanks TCP server; we won't be needing you any more
mng.kill()

We may now plot the closed-loop trajectories using matplotlib as follows

time = np.arange(0, sampling_time*simulation_steps, sampling_time)

plt.plot(time, state_sequence[0:4*simulation_steps:4], '-', label="position")
plt.plot(time, state_sequence[2:4*simulation_steps:4], '-', label="angle")
plt.grid()
plt.ylabel('states')
plt.xlabel('Time')
plt.legend(bbox_to_anchor=(0.7, 0.85), loc='upper left', borderaxespad=0.)
plt.show()

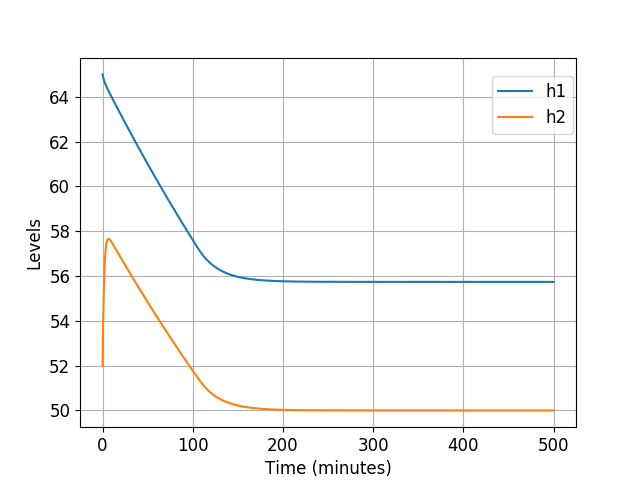
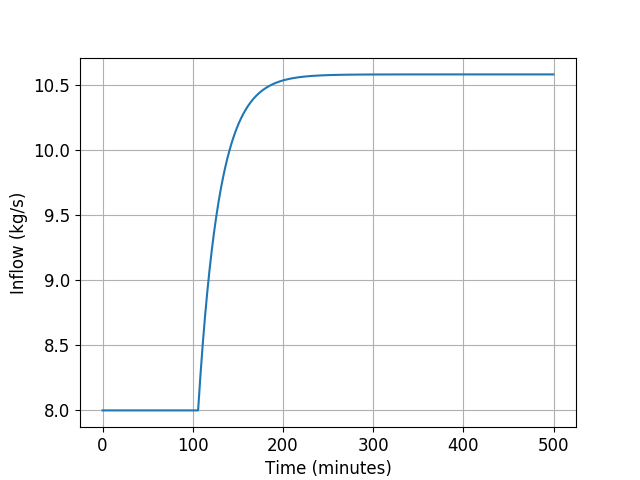
Solver statistics

In the above simulations, the average solution time is 134us and the maximum time is 1.77ms. We ran a second set of simulations with double the original prediction horizon, namely $N=240$, and the average solution time increased to 343us and the maximum time was 1.44ms.